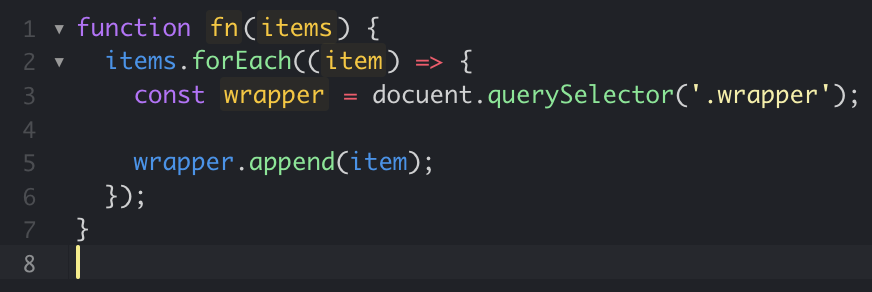
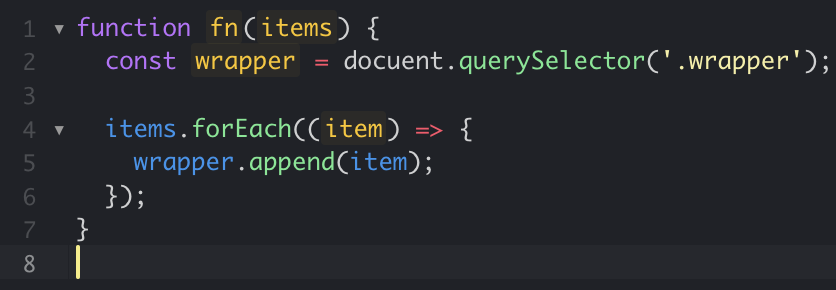
Big O Notation
Сложность и как её определить
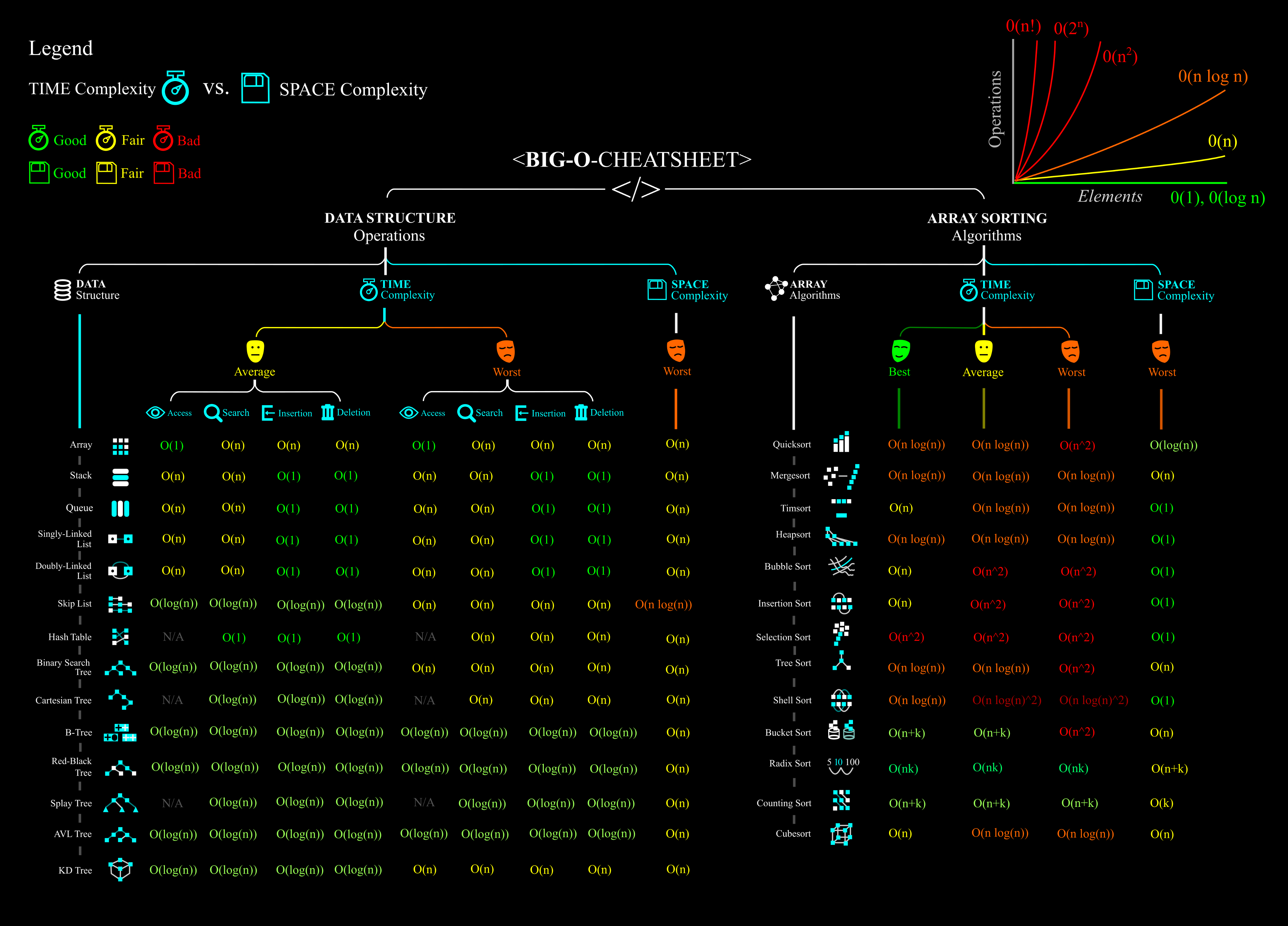
Сложность и как её определить
Сложность и как её определить



| Л | О | Л | |||
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | |||
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
| Л | О | Л | Л | О | Л |
Итого: 12 итераций и 9 дополнительных ячеек памяти.

| Л | О | Л | |||
| Л | О | Л | |||
| 0 | |||||
| 2 |
| Л | О | Л | |||
| 0 | |||||
| 2 |
| Л | О | Л | |||
| 0 | |||||
| 2 |
Итого: 1 итерация и 2 числа дополнительной памяти.
Однострочник:
4N итераций, 3N символов

С двумя указателями:
N/2 итераций, 2 числа

Зависимость объёма работы, которая выполняется алгоритмом, от размера входных данных, выраженная математической функцией.
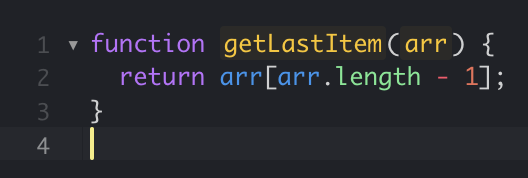
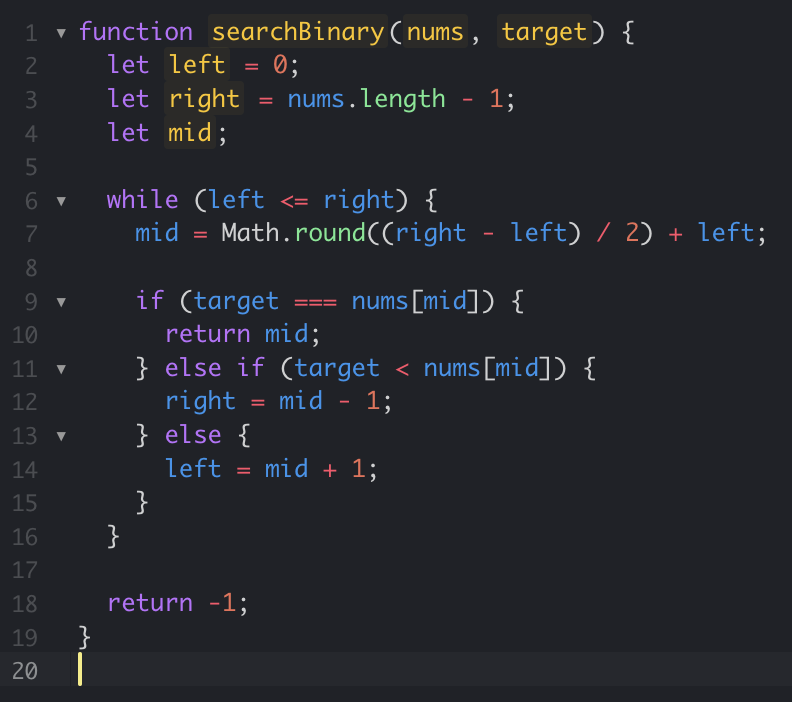
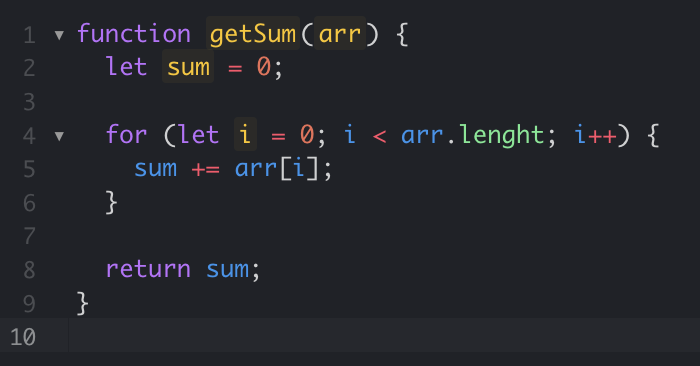

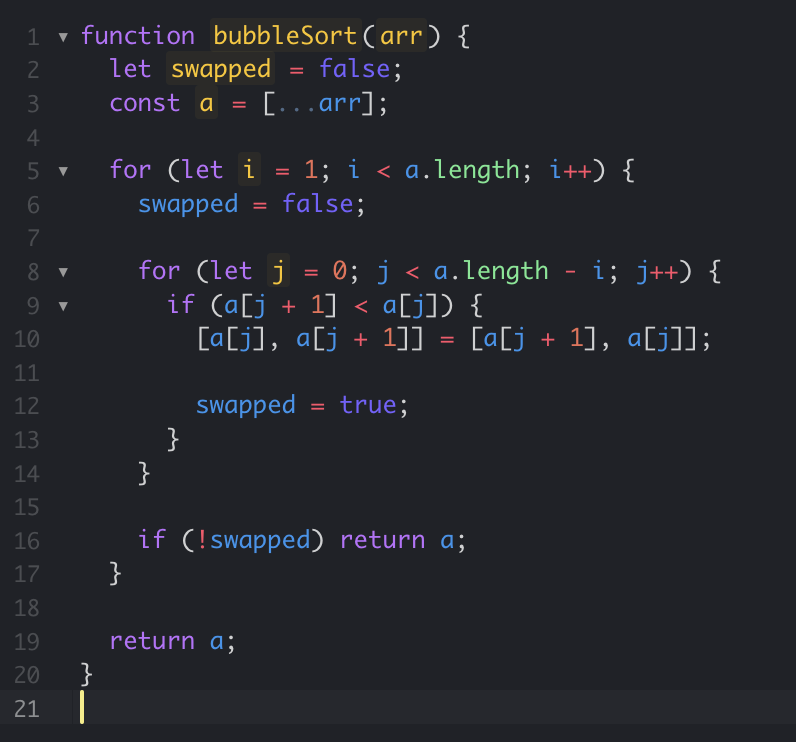
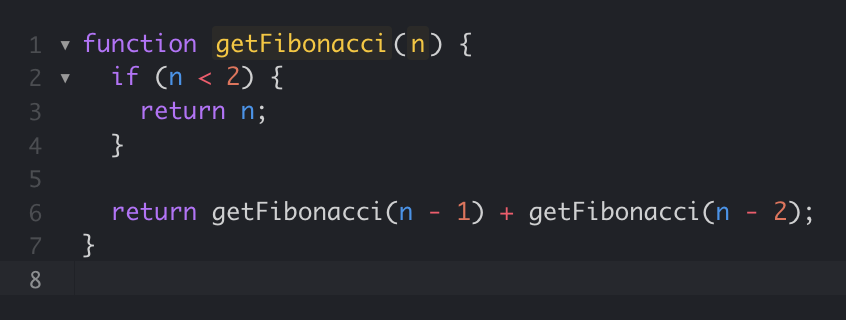
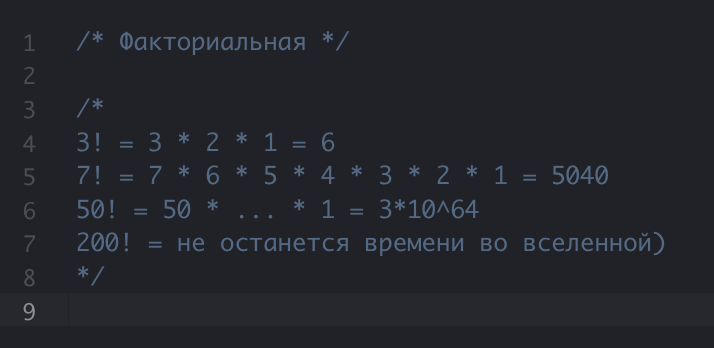
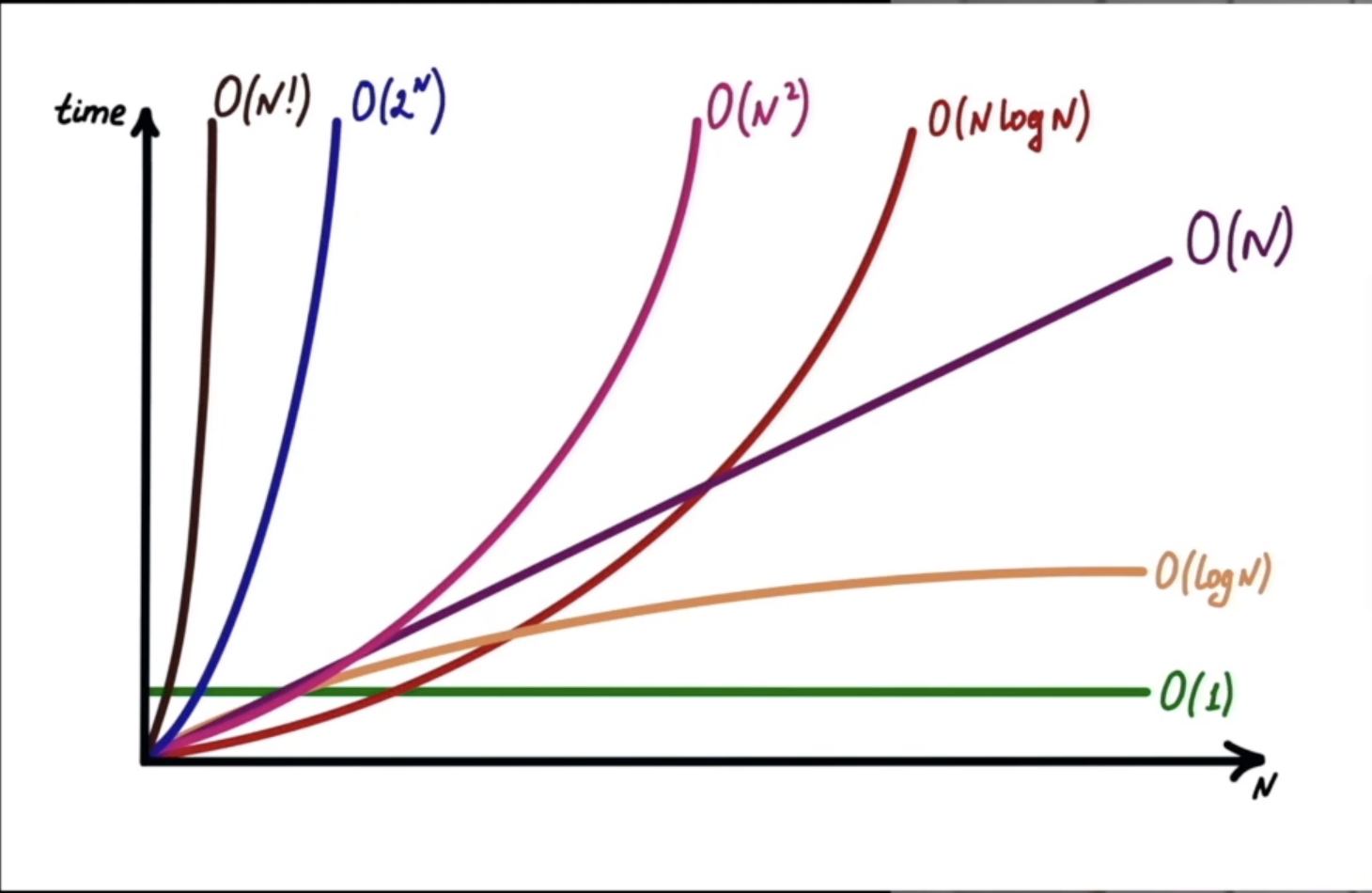

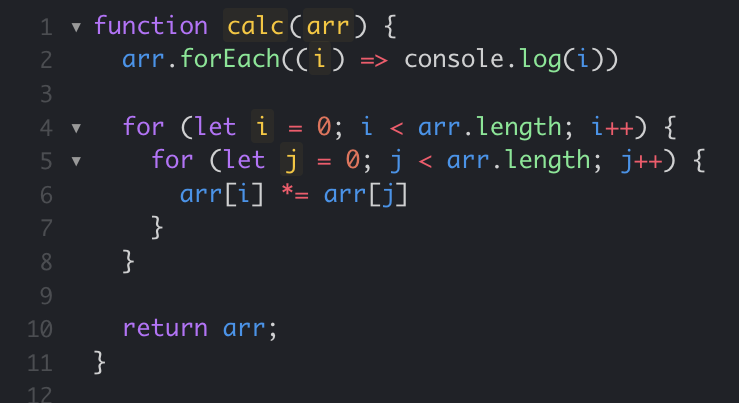
O(4N) -> O(N)

O(N/2) -> O(N)